本文为 “交叉熵”如何做损失函数？打包理解“信息量”、“比特”、“熵”、“KL 散度” 的笔记

神经网络在判断时所采用的标准与人不同，例如分辨一张图片是否是一只猫，我们无法将我们的判断标准详细的抽象出来让神经网络采用。因此我们只能尽可能让神经网络的标准和我们的判断标准接近，即相差越少越好。为了描述两个模型到底相差多少，而引出损失函数，损失函数就是相差多少的定量表达。

吴恩达给出了两个具体的表达式为：

在下面的最小二乘法与极大似然估计两小节中将对这两个公式进行解释。

最小二乘法

假设有识别图片是否为猫的模型，如下图所示。其中 $x_i$ 为人对图片的判断（是猫为 1，否则为 0），而 $y_i$ 是模型对图片的判断（选用 sigmoid 函数，值介于 0-1，可表示概率）。该神经网络的参数是 W,b

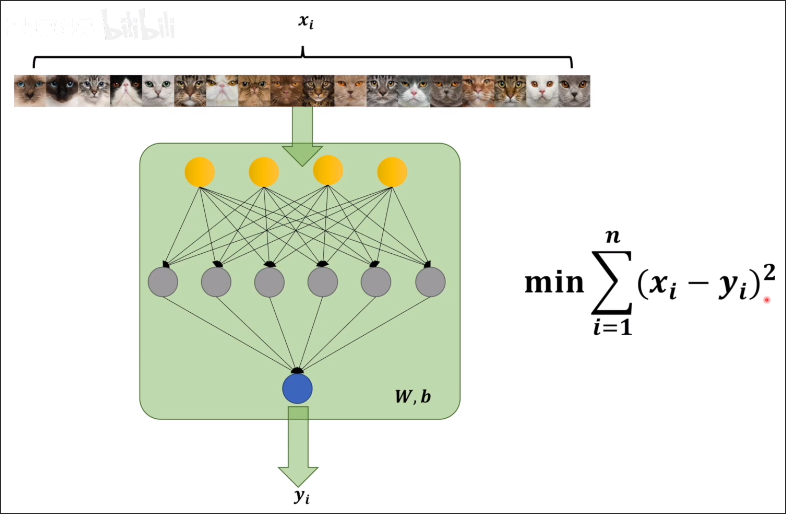
为了比较人脑中对猫进行判断的模型与神经网络模型的区别有多大，有一个最简单的办法就是直接对比人与神经网络分别判断的结果（$x_i$ 与 $y_i$ ），这两个值应该相差越小越好。因此我们可以优先考虑使用 $\sum_{i=1}^n |x_i - y_i|$。 但是使用绝对值会导致该函数在存在不可导的可能（例如 $|x|$ 在 $0$ 点处不可导）。所以我们可以采用下面这个公式：

这也就是最小二乘法的公式。

极大似然估计

假设我们想知道抛硬币结果的概率事件模型（当然现在我们知道正反的概率分别为 $1/2$ ），通过实验，我们抛了十次后，正面 7 次，反面 3 次。

通过这次实验我们虽然不能确定概率模型，但我们能够估计出到底是哪个概率模型的可能性更大，这个过程就是极大似然估计。

计算方法为 $P(C_1,C_2,C_3,...,C_{10}|\theta)$ ，该公式表示在概率模型为 $\theta$ 的情况下，同时发生事件 $C_1,C_2,C_3,...,C_{10}$ 的概率。

套用到最初的判断是否为猫的例子，有 $P(x_1,x_2,x_3,...,x_{n}|W,b)$ ，其中 $x_i$ 是我们打标签的结果，即第 i 个图片是否为猫。

$P(x_1,x_2,x_3,...,x_{n}|W,b)$ $= \prod_i^n {P(x_i|W,b)}$ 因为 $y_i=NN_{W,b}$ $= \prod_i^n {P(x_i|y_i)}$，其中 $x_i$ 属于伯努利分布 根据伯努利分布的概率公式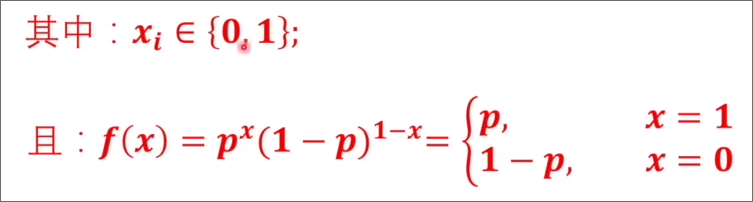： $=\prod_i^n {y_i^{x_i}(1-y_i)^{(1-x_i)}}$

之后为了方便求最大，我们可以先求 $\log$

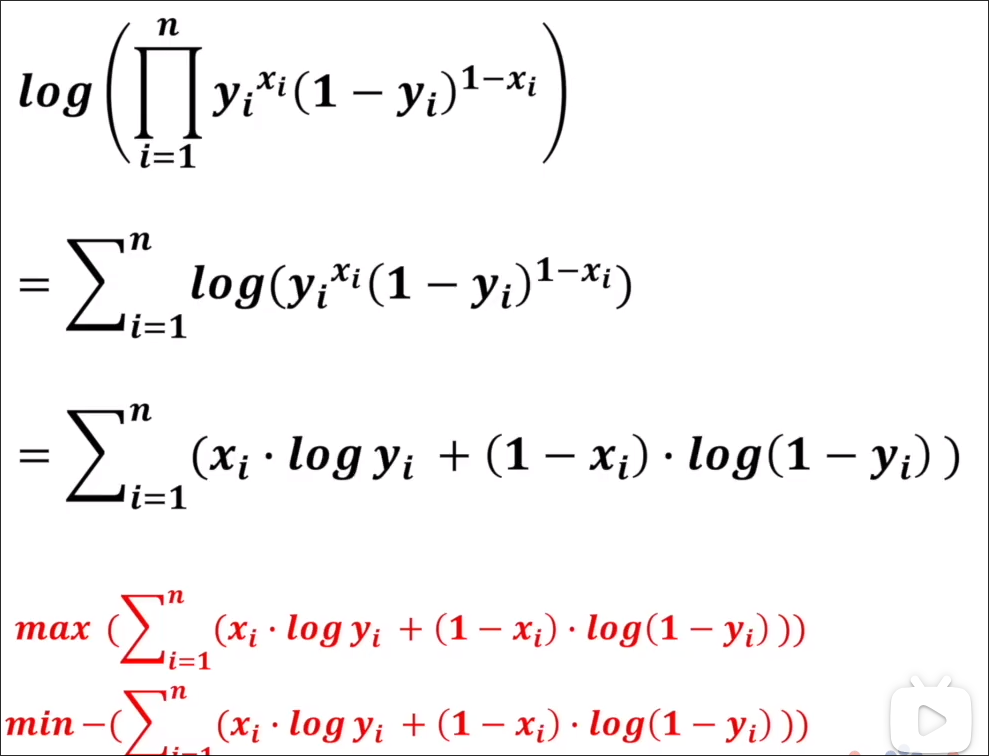
交叉熵

终极目标：让神经网络模型与人脑中的模型更相似

交叉熵也是用于比较模型之间差异的一种方法，具体来说，交叉熵通过先将模型换成熵这一数值，然后再用这个数值比较不同模型之间的差异。

信息量

在此之前我们先引入一个定义：信息量 假设有以下例子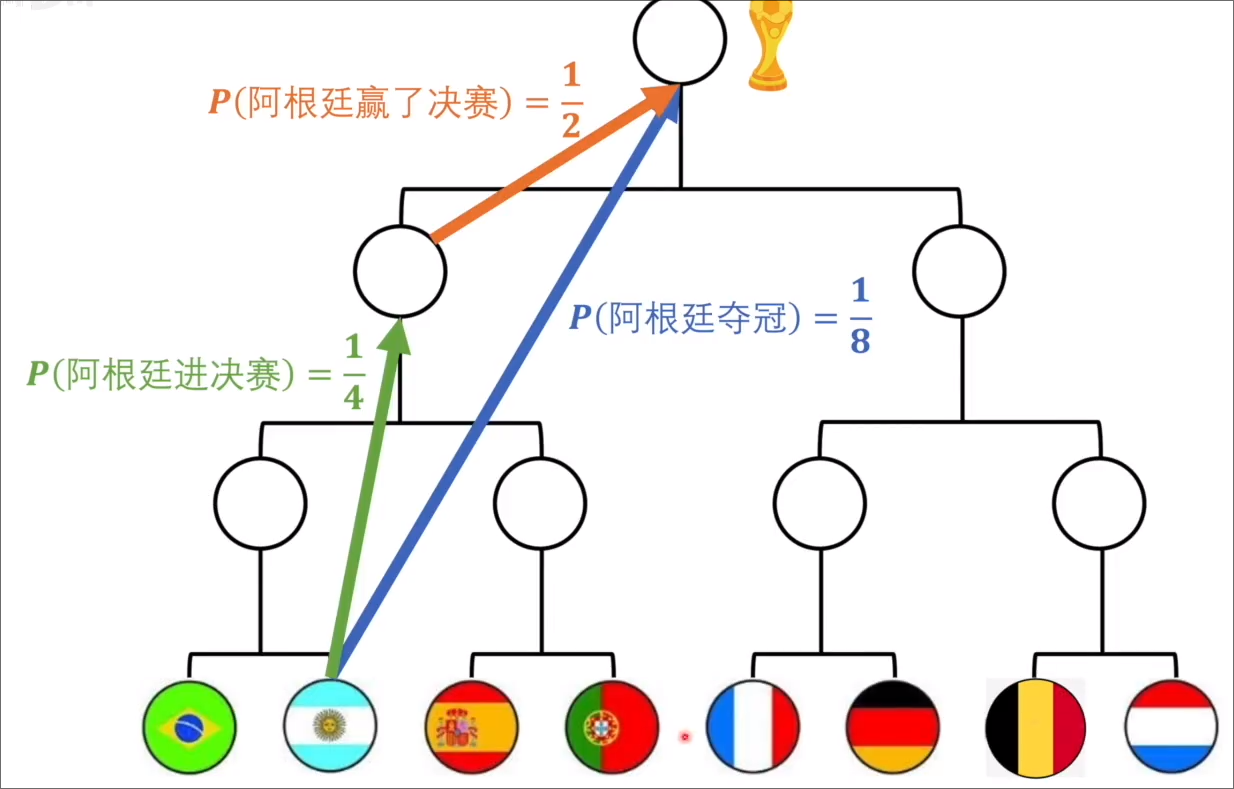： 其中 “阿根廷进决赛” “阿根廷赢了决赛” “阿根廷夺冠” 分别是不同的信息。由图可知，进决赛和赢了决赛的信息量之和应该等同与阿根廷夺冠（因为所传达的信息相同，并且都是从最初的 $1/8$ 的概率到 $100\%$ ）。

通过以上例子，假设有 f(x) := 信息量，将信息量定义为 f(x) 应该有：

当事件发生的概率越小时，不确定性越大，信息熵越大，所包含的信息越多，也就是说概率越小信息量越大

综上我们将信息量定义为 $f(x) := - \log_2 x$

计算机里的 n bit 数据，也可以表述为信息量为 n，例如要给计算机输入一个 16 位的数据，在输入之前这个数据的可能性为 $1 / 2^{16}$ ，它所具有的信息量就是 16

信息量可以表述为一个事件从不确定到确定所需要的难度有多大，例如确定一个 16 位的数据，需要通过确定 16 位每一位 0 和 1 的值。而熵也是来衡量一个系统由不确定到确定难度有多大。

例如，有如下两个系统 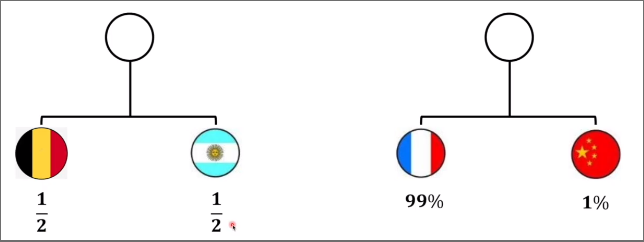以此计算各个系统的信息量为下图所示，其中乘以各自的概率是因为各个事件对整个系统的信息量的贡献应该按照其发生的概率计算。

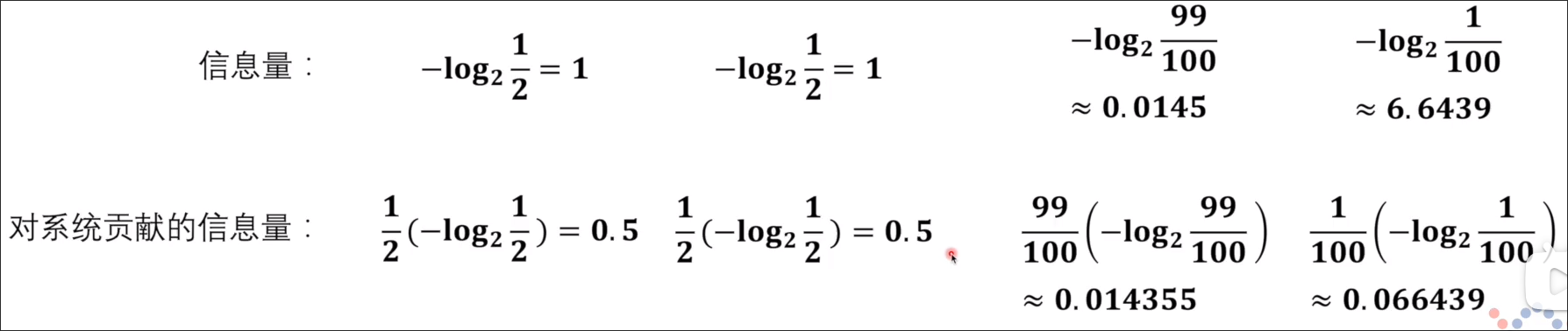
一个系统的信息熵可定义为，对各个事件的信息量求期望，即：

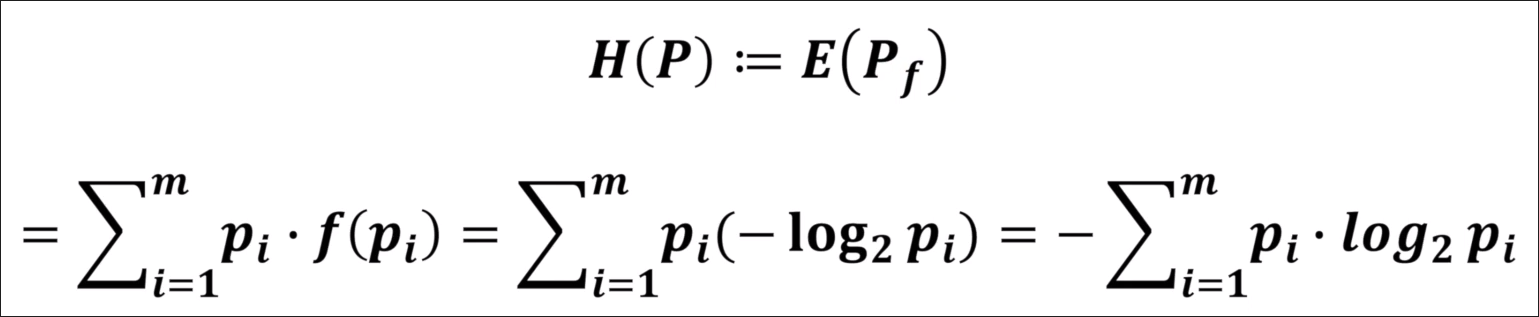
相对熵（KL 散度）

假设有两个系统 P 和 Q，求以 P 为基准的 KL 散度，公式如下 其中 $f_Q(q_i)$ 代表对于某一个事件 $q_i$ 在 Q 系统的中的信息量，第一行代表着求某一事件在 Q 中的信息量减去其在 P 中的信息量，并求它的期望。 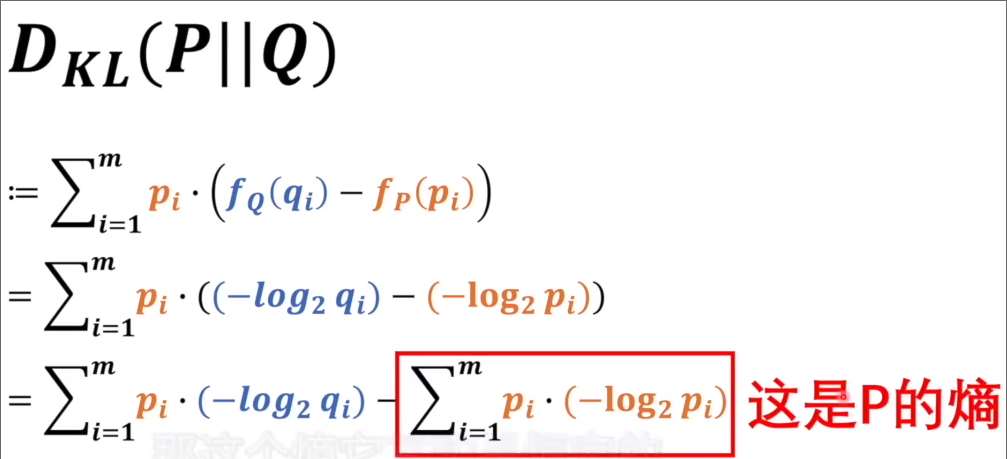其中减法前半部分就是交叉熵，可以用 $H(P, Q)$ 表达，根据吉布斯不等式KL 散度是大于等于 0 的，当 Q 和 P 相等的时候等于 0，当 Q 和 P 不等的时候一定大于 0，因此如果我们想让 P 和 Q 更接近的话（等同于让 KL 散度更接近 0），我们就需要找到让交叉熵最小的值，因此这个式子本身就可以作为损失函数。

交叉熵

交叉熵越小就代表着两个模型越接近，因此我们可以将交叉熵运用到神经网络里面。

由上一节所示，交叉熵的定义为 $H(P, Q)= \sum_{i=1}^{m} p_i (- \log_2 q_i)$ ，其中 m 为 P 和 Q 两个系统的事件数中最大的那个值，$p_i$ 代表第 i 个事件在 P 系统下的概率。

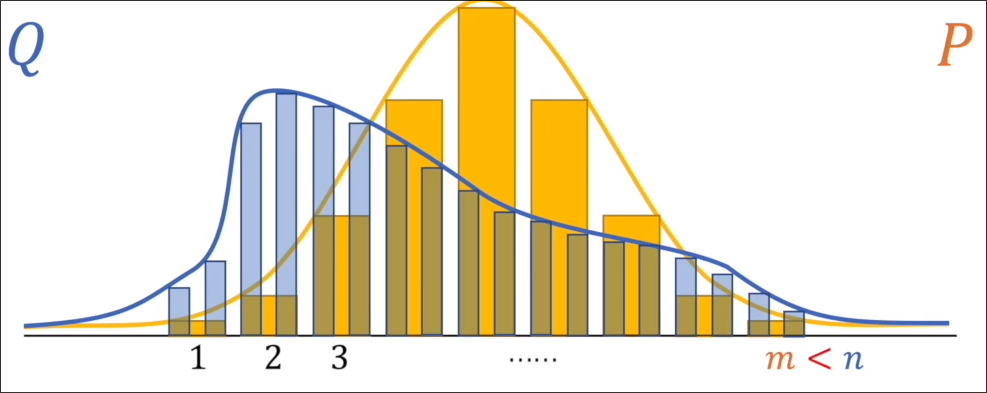
如图所示，Q 的事件个数 n 大于 P 的 m 则应该选择 n。

回到判断图片是不是猫的例子：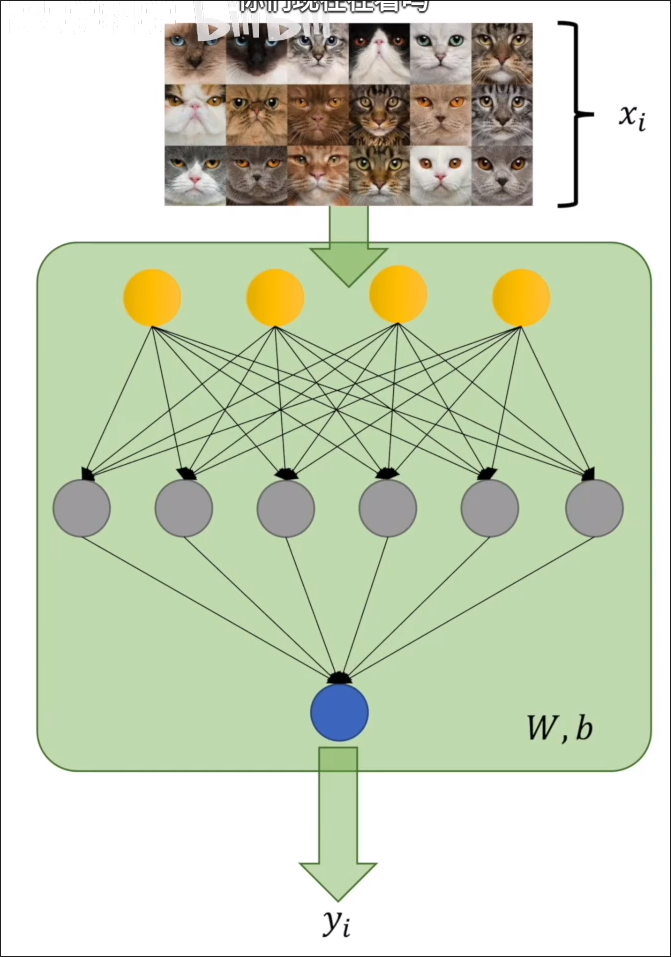

为了使人脑的模型和神经网络的模型更相似则可以利用交叉熵 $H(P, Q)$，有 $H(P,Q)$ $=\sum_{i=1}^2 p_i*(-\log_2 q_i)$ 其中 2 代表 P 和 Q 的事件数都是 2（是猫或者不是猫） $= x*\log_2 y + (1-x)*\log_2 (1-y)$ 这一步是因为$y$只代表着是猫的概率，而我们在当 $x$ 表示不是猫时，也要对应的乘不是猫的概率的信息量，即$\log_2(1-y)$ 。